
在量子力学中,物理系统的可观测量对应于算符,而这些算符需要是厄米算符,因为它们的本征值对应着实验中测量得到的物理量。厄米算符的特性保证了其本征值为实数,从而符合经典物理中测量结果为实数的经验事实。然而,这一约定是否可以从更深层次的原理上解释?同时,是否存在可观测的物理量具有复数值的情况?
在日常生活中,我们习惯于将测量结果表示为实数,无论是温度、距离,还是能量。这种直观的认知在量子力学中被抽象化为一个深刻的数学假设:所有可观测量都必须对应于具有实数本征值的厄米算符。然而,量子力学的世界并不总是符合直觉,例如波函数和许多中间计算结果往往以复数形式表达。既然复数在量子力学中如此重要,为何最终的可观测量必须是实数?
1. 可观测量实数性的数学基础
1.1 量子力学中算符与观测值的联系
在量子力学中,可观测量与线性算符一一对应。具体而言,量子系统的状态由希尔伯特空间中的态矢量 ∣ψ⟩ 描述,而物理可观测量对应的算符作用在该空间上。测量得到的观测值 λ 是的本征值,满足
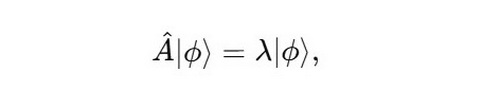
其中 ∣ϕ⟩ 是 的本征态。
1.2 厄米算符的性质
厄米算符是满足自伴随条件的线性算符,定义为
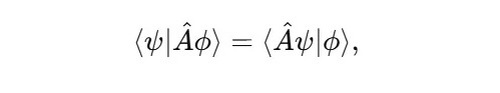
对任意态 ∣ψ⟩,∣ϕ⟩ 均成立。这一条件直接保证了厄米算符的本征值为实数,且其本征态形成一组正交基。这些数学性质奠定了可观测量的实数性基础。
1.3 为什么需要厄米算符?
如果观测量的算符不是厄米算符,其本征值可能是复数或复数域的一部分。然而,复数结果在物理测量中没有明确的现实意义。例如,如果测量一个粒子的能量为复数,这不仅无法通过实验解释,还可能违反能量守恒等基本物理定律。因此,要求观测量算符为厄米算符成为量子力学的基本假设之一。

2. 可观测量实数性的物理意义
2.1 测量结果与实验一致性
实验测量结果需要与现实一致。在经典物理中,测量值是实数,因此量子力学也继承了这一基本约定。实数观测值的假设使得量子力学的测量结果可以直接与实验数据对应。
2.2 复数量在量子力学中的地位
尽管最终的观测值是实数,但复数在量子力学中无处不在,例如:
波函数 ψ(x,t) 通常为复数,其模平方是概率密度,观测值总是实数。
干涉现象中,复数振幅的相位差直接影响实验结果,但测量值仍是实数。
2.3 实数性是否可以被突破?
在量子理论的框架下,实数性是观测量的基本性质,但这并不排除某些理论可能允许复数观测量。例如,在扩展的理论模型中,复数观测值可能反映比经典测量更深层次的物理特性。

3. 复数观测量的可能性与挑战
3.1 黎曼-西尔伯斯坦矢量的例子
黎曼-西尔伯斯坦矢量是一个复值矢量,用于描述电磁场:
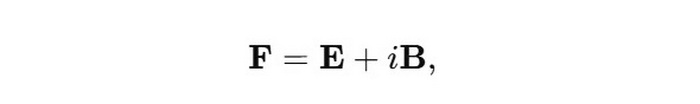
其中 E 是电场,B 是磁场。虽然它在量子光学中有重要应用,但作为复数,它并不对应直接可测的物理量,而是作为数学工具简化计算。
3.2 复数观测量的定义尝试
要定义复数观测量,需重新考虑量子力学的测量理论。例如,将观测值视为复平面上的点,但这可能导致概率解释的不一致性,进而挑战当前的量子力学框架。
3.3 实验限制与理论障碍
现有实验技术的限制和理论假设(如波函数坍缩的实数性)使得复数观测量难以被验证。此外,引入复数观测量可能导致理论模型的非物理性,例如违反概率守恒。
4. 可观测量实数性背后的哲学思考
4.1 实数是否唯一适合描述现实?
实数的连续性与物理量的连续性似乎契合,但量子力学的离散性也表明实数可能并非唯一选择。复数、四元数甚至其他数学结构可能在更高层次的理论中被采用。
4.2 实数性是否只是约定?
可观测量的实数性是否源于实验数据的限制,而非物理规律的必然?这一问题在解释性理论(如弦理论或量子引力理论)中可能有新的视角。
结语
可观测量实数性是量子力学的基本假设之一,其数学依据来自厄米算符的实数本征值,其物理意义在于与实验结果的一致性。然而,这一假设并非不可突破。复数物理量的存在,以及它们在理论与实践中的应用,显示了量子力学框架的潜在扩展性。未来的研究可能揭示复数观测量的深层物理意义,为量子理论开辟新的方向。
【声明】以上内容只代表原作者个人观点,不代表artda.cn艺术档案网的立场和价值判断。

